With over 35 years in management, science, and consulting, Dr. Klaus Radermacher KRBE GmbH brings a wealth of experience in analyzing and assessing transportation systems. His innovative approach integrates infrastructure and movement processes into holistic CO2 and energy comparisons.
Follow Dr. Klaus Radermacher’s LinkedIn newsletter “Think. Mobility. Differently.” for regular insights on mobility concepts and transportation systems.
The views and opinions expressed in this column are solely those of the author and do not necessarily reflect the official policy or position of AeroTime.
One cannot talk about mobility and try to develop innovative and efficient transportation systems without being aware of some basic physical facts. In the following text I will try to present these in a very general way, but for readers interested in further details the most relevant physical formulas are listed at the end.
Physics of mobility 101
Every movement, every transportation, regardless of whether it takes place in a car, by train, on a bicycle, in an airplane or simply by walking, requires energy.
Energy is always required
- for acceleration,
- to overcome air drag, as well as rolling and friction resistance of wheels on road and rail,
- and for “lifting work”, i.e., working against gravity.
It must be noted that energy to overcome air drag is only required when the movement takes place in an atmospheric environment. Outside an atmosphere, e.g., on the way to the Moon or other planets, or even in outer space, there is no air drag, as soon as the Earth’s atmosphere has been left behind. This is why research orbiters can travel ‘forever’ through space once they have been accelerated sufficiently and are outside any significant atmosphere. Further considerations in this text are restricted to land-based and air travel on this planet.
The following parameters are decisive for the total energy required for a transportation process:
- the speed at which the means of transportation moves and to which it must be accelerated,
- the total mass to be moved,
- the number of acceleration processes that occur during the transportation process between origin and destination,
- the total elevation (altitude) to be overcome during the transportation process for which lifting work must be performed.
The mass to be moved (in kilograms, kg) plays a decisive role both in the energy required for acceleration and for the lifting work. The speed (in kilometers per hour, km/h) is one of the relevant variables for the energy required for acceleration and for overcoming air drag. The shape of the means of transport (the more streamlined the better), which is included in the calculation formula as the cd value (air drag coefficient), the air density r (Greek letter rho, in kg/m³), which decreases approximately logarithmically with increasing altitude, and the “frontal area” of a vehicle or the wing area of an aircraft are also important for air drag. It is important to understand that speed influences both the acceleration energy and the energy required to overcome air drag as a quadratic variable. Twice the speed requires four times the energy.
At speeds of around 80km/h (50mph) and above, the air drag becomes so great in relation to the rolling and frictional resistance of land-based means of transport that the latter can be largely ignored for energy calculations. We will therefore not go into these variables any further at this point.
What is of great importance, however, is that the physical calculations for overcoming air drag are based on the assumption that the means of transportation can easily push away the air against which it is fighting. This assumption is correct, unless you are in a comparatively narrow enclosure, such as a railroad tunnel. Since tunnels for high-speed lines must always be built as a single track tube for safety reasons from a length of 500 meters and longer and therefore just fit around the train, it is necessary here that the air, which cannot escape to the side due to the tunnel walls, must be pushed forward towards the tunnel exit like a piston that is getting bigger and heavier. Depending on the length of the tunnel and the speed of the train, this means that the amount of energy required to overcome the air drag when passing through the tunnel can easily be twice as much or more compared with traveling across an open field.
What masses need to be moved?
Let us now look at the mass that has to be moved for each passenger depending on the transport system. For a passenger, a mass of 100kg including luggage is generally assumed as the ‘payload’, to which the proportional weight of the means of transport must then be added.
An average car weighs 1,500kg; statistically speaking, there are (only) 1.5 people in it when it is being driven, so we are dealing with one ton of vehicle weight per passenger. Additionally, about 17kg of fuel in the tank per person must be included, so we have 1,117kg of mass per person for mobility in MIT (motorized private transport); quite a lot, considering that the payload is only 100kg.
An empty ICE train (a German high-speed train) weighs 408 tons. Before COVID-19, Deutsche Bahn trains had an average occupancy rate of 56%, meaning just over half the seats were typically filled.
At this level of occupancy, approximately 1,700 kg (1.7 tons) of the train’s weight corresponds to each passenger. When you add the passenger’s own weight (estimated at 100 kg, including luggage), a total of 1,800 kg (1.8 tons) must be moved for each person on board. Incidentally, the average capacity utilization of trains in Switzerland is only around 28%. If we take the SBB RABe 502 (aka FV-Dosto, TWINDEXX Express) from Bombardier, which is widely used there, as an example, more than 2.5 tons of train weight must be moved per passenger. In these examples, we assume trains are electric, so no fuel must be carried. In case trains run on diesel, the average amount of diesel in the tank would have to be added to the overall mass.
For aviation, we take an Airbus A321 as a basis, a rather large plane for domestic air travel. We then have to distribute the empty weight of 47.5 tons to the number of passengers based on an average load factor (utilization). This results in a total aircraft weight of around 290kg per passenger. In addition, there is an average of 57kg of kerosene per passenger in the tanks at the time of takeoff, so that ultimately a mass of slightly under 450kg per passenger must be accelerated and moved.
We see that an average-loaded train has to move four times the mass per passenger compared to an average-loaded domestic flight. This fact has a significant influence on the amount of energy required for acceleration and lifting work.
Energy calculations
The energy required for acceleration depends not only on the mass but also on the final speed. The speed is included in this calculation as a square; doubling the final speed requires four times the acceleration energy. Accelerating a mass of 1,117kg (one person in a car) once to 130km/h requires 728kJ (kilojoules) of energy. Accelerating this mass to 180km/h requires around 1,400kJ, almost twice as much. Accelerating a passenger on a train (1,800kg) to 270km/h requires 5,063kJ; accelerating a passenger (450kg) to around 880km/h on a plane adds 13,525kJ to our energy bill for the flight. These examples clearly illustrate what the quadratic component of final speed input means in the calculation.
But our considerations are not over yet. Let’s compare a journey from Hamburg to Munich. In an airplane, we have exactly one acceleration process at takeoff, while the train stops at least eight times at train stations in between even with the fastest connection. We have another acceleration process from 0 to 270km/h (or more) after each stop at the station, so compared to just over 13,500kJ for the acceleration of the plane, at least 45,567kJ is on the energy bill just for acceleration on the train. From Hamburg to Zurich there are even more stops on the way and thus 14 acceleration processes are required, just after stopping at the stations.
Added to this are all the additional acceleration processes caused by varying maximum speeds along the route. The same applies to traveling by car; dozens, sometimes hundreds, of changes in speed caused by the route and traffic result in an extremely inefficient motion sequence from a physical and energy point of view.
We recognize an important physical principle here: the more uniform the movement, the fewer accelerations, and decelerations, the more efficient the movement is from an energy point of view. Traffic must flow! Air travel, which is usually point to point with no intermediate stops, has a significant advantage over land-based mobility systems regarding movement efficiency.
However, with electrically powered transportation systems, it is possible to convert some of the kinetic energy back into electrical energy when slowing down and return it either to a battery (electric cars) or to the power grid (trains). This is already being used in many ways, but the effects are and remain comparatively small and are disproportionate to the energy previously required for the many acceleration processes.
The issue of frequent, system-related acceleration processes in rail and road transport is supplemented by the usually significantly greater distances that have to be covered between two locations in order to get from the starting point of a trip to its destination.
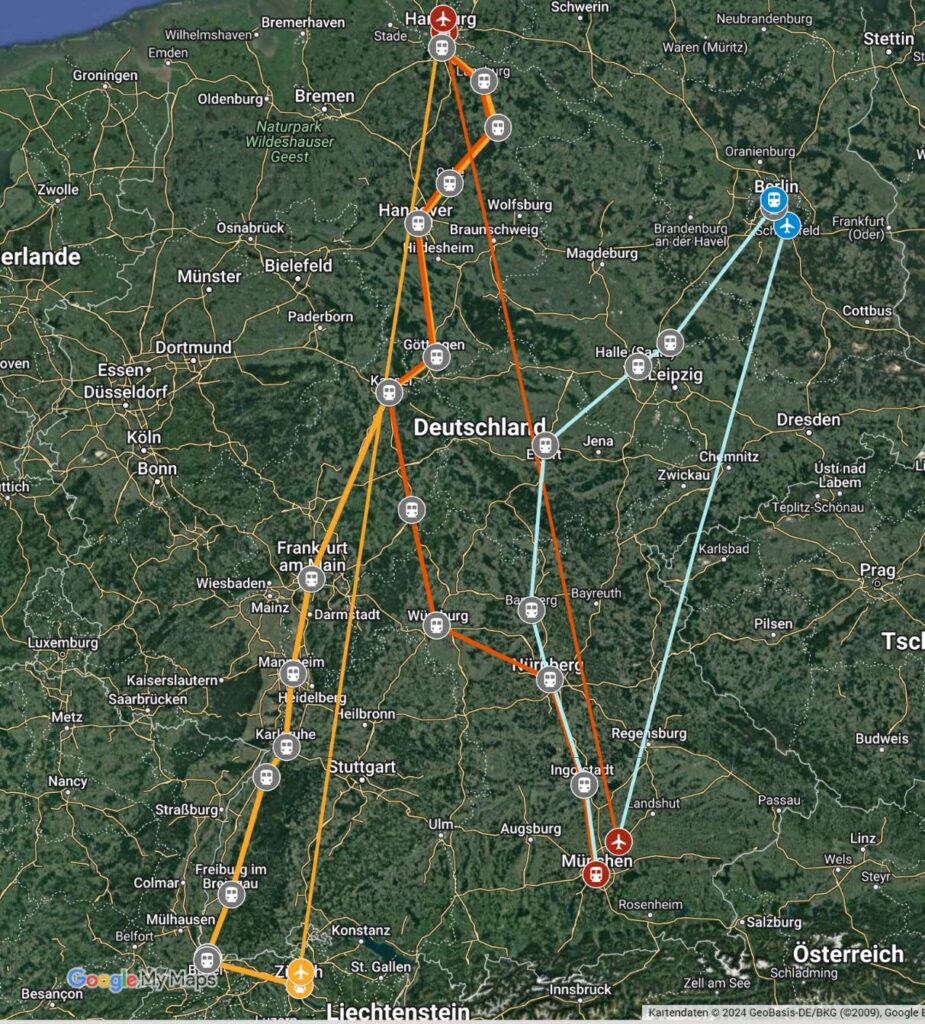
The map shows a number of classic routes (Hamburg-Munich, Hamburg-Zurich, Berlin-Munich) for the fastest train connection compared to the route for aircraft, as the crow flies. The land routes are between 30% and 35% longer. To be fair, it must be stated that aircraft do not always travel the shortest possible distance between two airports due to fixed arrival and departure routes and air traffic control requirements. However, the resulting route extensions are still significantly shorter than traveling by train or car.
The energy required for the aforementioned lifting work also depends on the mass, and the altitude at which the mass must be lifted. Lifting work is not only required for airplanes, but also for land-based means of transport as soon as they have to overcome an incline, even if they never take off from the road or rail. For car drivers, this is immediately apparent from the fuel consumption display when driving uphill.
The total difference in altitude to be overcome on the route is relevant. Since only just under a quarter of the mass per passenger has to be moved in an airplane compared to a train, the total energy required for the lifting work on the Munich-Hamburg route is also lower, even though the airplane climbs to an altitude of around 10,000 meters. Although trains and cars always remain on the ground and must cope with significantly smaller differences in altitude, they have to use more energy for lifting work due to their greater mass. Specifically for our example from Hamburg to Munich, for a passenger with a total mass of 447kg and an assumed cruising altitude of 10,000 meters, 43,851kJ of energy must be expended for the lifting work. The ICE train on the same route only has to cope with lifting work for a total of 2,599 meters, but since an average of 1.8 tons needs to be moved for each individual passenger, the energy adds up to 45,893kJ, more than for a passenger in a plane. Who would have expected that? Yes, doing the math by applying the laws of physics sometimes leads to surprising results.
Calculating the amount of energy required to overcome air drag is far more complex. The exact cd value for the vehicle must be known, the air density which depends on temperature and altitude, and the specific situation changes with every minimal change in speed relative to the surrounding air. In the case of rail travel, tunnels passed through at high speed are also very inefficient from an energy point of view. It is important to understand that air drag must be overcome continuously during a transportation process, so the amount of energy required for this must be calculated for each PKM (passenger-kilometer) covered. The shorter the distance, the better.
If we assume a car with a frontal area of 3 m², a cd value of 0.3 and an air density of 1.225kg/m³ in road traffic, this results in a value of 479kJ per PKM for overcoming air drag at 130km/h with an average load of 1.5 people in the vehicle. At 180km/h, this is already 919kJ in the same car under the same conditions. In aviation, the high speeds do have a negative effect on these calculations; on the positive side, the air density at the cruising altitude of aircraft is only around 35%-40% of the density on the ground. The cd value is also significantly lower, but the relevant wing area is significantly larger than the frontal area of a car. High-speed trains are also more streamlined than the vast majority of cars, but their length of several hundred meters results in a comparatively high cd value, and they also have to fight their way through the much denser air at ground level.
In summary, it can be said that the lower the total mass to be moved and the lower the number of acceleration processes that must be carried out, the more energy-efficient a movement process is. The rail and road transport systems in particular have considerable potential for optimization in this respect with regard to their current usage.
What’s the bottom line?
Looking at and comparing different mobility and transportation systems from a physics’ perspective leads to interesting results. Having to move around a much lower mass per passenger compared to driving in a car or riding on a train is a great advantage. The fact that aviation manufacturers have been working on weight reductions for decades is a great benefit over other mobility systems, especially since there is still a tendency for new generations of cars to become heavier than in the past. Electric vehicles are particularly bad at this, since the batteries alone are always good for several hundred kilograms of extra weight, which always needs to be moved, accelerated and lifted. The much higher speed of aircraft, however, is responsible for a higher energy consumption to overcome the air drag, despite the lower air density at cruising altitudes of aircraft. On the other hand, not having to follow land-based paths allows for a considerable shorter distance to be overcome between two points.
At several hundred kilometers, transporting 180 passengers at the average utilization rate in a modern, fuel-efficient plane is far more energy efficient than driving the same distance with 120 average cars with average utilization. Even the train ride is not necessarily more energy efficient. In addition to that, the plane does not need any route infrastructure (highways, streets, train tracks) between its nodes (airports), the air does not need to be built. Route infrastructure for cars and in particular for trains is an immense source of CO2, which needs to be included in the overall CO2 calculations for mobility systems and finally needs to be attributed to the traffic performance in PKM. Especially, when there is little demand on certain routes, the CO2 costs per PKM increase dramatically, as the CO2 emissions from construction are independent of the usage over the years.
There is absolutely no reason to condemn or glorify certain mobility systems. They all have their justification. It is always helpful to look at facts and figures from a science and engineering perspective. Ideology and emotions will not get us to the solutions we urgently need.
Appendix: Formulas for physics buffs
Energy for acceleration: 0.5 * m * v²
with m: mass in kg, v: speed (velocity) in m/s (meters per second).
Energy for lifting work: m * g * h
with m: mass in kg, g: gravitational constant = 9.81 m/s2 , h: altitude in m.
Energy to overcome the air drag: 0.5 * r * cd * A * v²
with r: air density in kg/m³, cd : drag coefficient, A: frontal area of the vehicle, for airplanes wing area, v: speed in m/s.

